![[Home]](https://ludism.org/logo/sclogo160.png)
Lines of Action is a two-player abstract strategy board game invented by Claude Soucie.
It was given wider dissemination and positive publicity by its inclusion in Sid Sackson's book A Gamut of Games, but for many years no stable playing community developed to explore the strategy to any depth. Only starting in the 1990s has any deep understanding of the game evolved.
In the last few years, not only has the play of the best humans risen dramatically, but simultaneously excellent computer programs have emerged. The level of play is improving both among humans and computers, but for the present the strongest LOA-playing entity in the world is probably one of the two programs YL or Mona written by graduate students at the University of Alberta.
Mona has been dominant at slower correspondence games, and YL successfully defended its tournament title against other computers at the 7th Computer Olympiad in Maastricht in the summer of 2002.
The best human players are Jorge G?mez Arrausi and Kerry Handscomb. Jorge has played competitive games against top computer programs, but hasn't been able to triumph in recent matches.
Claude Soucie, the inventor of LOA, died just as his game was beginning to reach a critical mass of interest. Some of the finer points of the rules are just now being standardized, without the benefit of appeal to Soucie. In all situations which were discussed by Sackson, his presentation is now generally accepted as authoritative.
LOA is played on a standard chessboard, with the same Algebraic chess notation|algebraic notation for ranks and files. Each player controls twelve checkers, which are initially arrayed as follows:
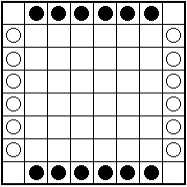
The object of the game is to bring all of one's checkers together into a contiguous body.
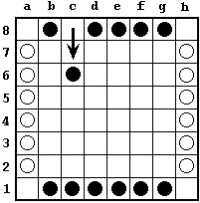
Players alternate moves, with black having the first move. Checkers move horizontally, vertically, or diagonally. A checker moves as many spaces as there are checkers (both friendly and enemy) on the the line in which it is moving. For example, black may open with c8-c6. His checker moves two spaces because there are two checkers in the line (c8-c1) in which black is moving.
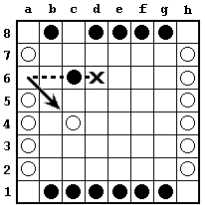
A checker may not jump over an enemy checker. Thus in the above diagram, white can't play a6-d6, even though there are three checkers in row 6. White might instead play a6-c4, moving two spaces because there are two checkers in the diagonal (a6-f1) in which white is moving.
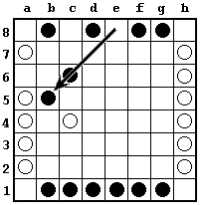
A checker may jump over friendly checkers. Thus black may continue with e8-b5, jumping his own checker. He moves three spaces because there are three checkers in the diagonal (a4-e8) in which he is moving.
A checker may move to a square occupied by an enemy checker, resultung in the latter's capture and removal from the game. For example, white may play h3-f1, capturing the black checker on f1.
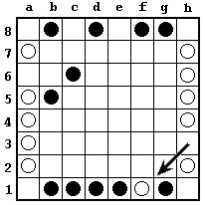
A player who is reduced to a single checker wins the game, because his pieces are by definition united. If a move results, due to a capture, in each player having all his pieces in a contiguous body, then the player making the move wins. For example, in the diagram below, white to move could win with the capture h8-g6, even though that results in both players having entirely connected formations. Black to move could win with either f6-f4 or f6-d4.
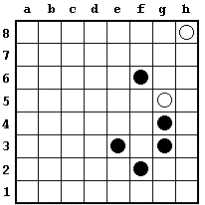
The game can become quite tactical in open postions where the checkers on both sides are mobile. The strategic depth of the game, however, derives to a large extent from blocking strategies designed to limit the opponent's mobility. It can be very advantageous to pin one or more enemy checkers against the side of board by moving in the second row or column.
Having more checkers is usually an advantage, because they can limit the opponent's options as they mass together. On the other hand, material considerations are not all-important, because having fewer checkers also means having fewer to unite.
The above moves illustrated the rules, but not necessarily good play. The following moves are more typical of expert play.
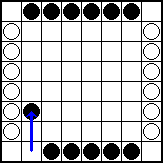
Black plays b1-b3. The checker moves two squares vertically, because there are two checkers in the file: b1 and b8. This move gives white no opportunity to capture, and threatens to hem in the pieces on the a-file.
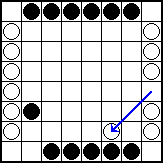
White moves h4-f2. The checker moves two spaces because there are two checkers in the diagonal: h4 and e1. White threatens the mobility of black's checkers in the bottom row.
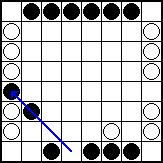
Black plays d1:a4, jumping over his own checker (which is permitted) and capturing the white checker at a4. Note that black moved three spaces, as there were three checkers in the diagonal: a4, b3, and d1.
It isn't clear whether the capture is advantageous or not. Black does now have an extra checker, but the move didn't do much to block white or build a central mass for black. Usually early captures on the edge are not especially powerful, whereas early captures in the center are extremely good.
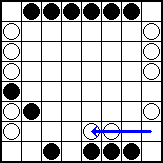
White plays h2-e2, continuing the blockade of the first rank. The checker moves three squares, jumping over a friendly checker. White, despite the substantial disadvantage of moving second, apparently is in the lead now due to the reduced mobility of black's first-row checkers. White will soon play a2-d2, continuing to build his own bridge and forcing black's checker on e1 to move sideways if it wants to join the game.
Lines of Action inspired Sid Sackson to develop another game, entitled Fields of Action.
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Lines of Action".